'회귀 분석'이라는 단어를 처음 접했을때, 도저히 의미를 알 수 없었다(다른 용어들도 크게 차이는 없지만)
'한 바퀴 돌아 제자리로 돌아오거나 돌아감' 회귀回歸의 사전적 뜻이다.
이 뜻과 같이, 회귀분석이란 평균보다 크거나 작은 값들이 평균으로 돌아간다는 가정을 이용한 분석이다.
이는 Galton 이라는 학자가 아버지의 키로부터 아들의 키를 예측하는것에서 시작하였다.
'아버지의 키가 크다면 아들도 키는 큰 편이지만 아버지보다 조금 작아 평균에 가까워지고, 아버지의 키가 작다면 아들의 키는 작은 편이지만 아버지보다 조금 커져 평균에 가까워진다'는 가설을 세웠고, 이것에 대한 분석방법을 회귀(regression)이라고 하였다.
선형회귀는 결과변수 y와 원인변수 x의 선형 상관 관계를 모델링 하는 것이다.
즉, x값이 주어졌을때 이를 가장 잘 나타낼 수 있는 y값을 얻을 수 있는 모델링이다.
$$ y_{i} = \beta + \alpha \cdot x_{i} + \epsilon $$
$$ \hat{y_{i}} = \beta + \alpha \cdot x_{i} $$
이때, 만약 결과의 원인이 하나가 아닌 여러개(원인변수가 여러개)라면 다중회귀 분석이라고 한다.
$$y_{i} = \beta_{0} + \beta_{1} \cdot x_{1} + \beta_{2} \cdot x_{2} + \cdots + \beta_{n} \cdot x_{n} + \epsilon$$
우리는 단순회귀분석과 다중회귀분석에서 각각 위와 같은 식을 가정할 수 있고, 데이터로부터 x값이 주어졌을때 예측값 $\hat{y_{i}}$를 얻을 수 있다. 하지만 하나의 선으로 모든 y값을 정확히 나타낼 수 없기 때문에 우리가 예측한 $\hat{y_{i}}$와 실제 데이터 $y_{i}$에는 차이가 존재한다. 이러한 차이를 오차(Error)라고 하며 $\epsilon$으로 표기한다.
여기서 우리가 원하는 것은 해당 식에서 오차가 가장 최소가 되도록 하는(x값을 해당식에 대입했을때 예측되는 값과 실제 값의 차이가 최소가 되도록 하는) $\beta$값과 $\alpha$값을 찾는 것이다.
SSE
SSE란, Sum of Squared Error의 약자로 오차의 제곱값을 합한 것이다. 이때 우리가 원하는 것은 위에서 언급한 듯이 SSE를 최소화(Minimize)하는 $\alpha$와 $\beta$값이다.
$$ y_{i} = \beta + \alpha x_{i} + \epsilon \quad \epsilon = y_{i} - \beta - \alpha x_{i}$$
$$ SSE = \sum(\epsilon^{2}_{i}) = \sum(y_{i} - \beta - \alpha x_{i})^{2}$$
위 식에서 $\epsilon$은 우리가 모르는 미지수 $\beta$와 $\alpha$ 각각에 대한 2차식이다.
우리는 중학교때, 미지수 x에 관한 2차식에서 최소가 되는 점을 구하는 방법을 배웠다. 바로 기울기가 0이 되는 지점이다.
따라서 우리는 미지수 $\beta$와 $\alpha$각각에 대한 2차식에서 각 미지수의 미분값이 0이되는 $\beta$와 $\alpha$를 구하면 된다.

OLS
OLS란, Ordinary Least Squares의 약자로, 앞서 말한 오차의 제곱을 최소화 하는 $\beta$와 $\alpha$를 추정하는 방식이다.
먼저, 단순 선형회귀부터 알아보자. 그전에 $\sum$ 식의 특징을 모른다면 먼저 아래를 열어서 확인
단순선형회귀(Simple Linear Regression)
$$\frac{\partial SSE}{\partial \beta} = 2 \sum(y_{i} - \beta - \alpha x_{i})(-1) = 0 \; (1)$$
$$\frac{\partial SSE}{\partial \alpha} = 2 \sum(y_{i} - \beta - \alpha x_{i})(-x_{i}) = 0 \; (2)$$
(1)번식에다가 $\times \bar{x}$를 하면 (3)
$$n \bar{x} \bar{y} = \alpha \bar{x} \sum x_{i} - \beta \sum x_{i} \; (3)$$
$$\sum x_{i} y_{i} = \alpha \sum x^{2}_{i} - \beta \sum x_{i} \; (4)$$
이제 (4) - (3)하면,
$$\alpha (\sum x^{2}_{i} - \bar{x} n \bar{x}) = \sum (x_{i}y_{i}) - n \bar{x} \bar{y}$$
$$\hat{\alpha} = \frac{\sum x_{i}y_{i} - n \bar{x} \bar{y}}{\sum x^{2}_{i} - n \bar{x}^{2}} = \frac{\sum (x_{i} - \bar{x})(y_{i} - \bar{y})}{\sum (x_{i} - \bar{x})^{2}}$$
이렇게 x의 계수 $\alpha$의 예측값 $\hat{\alpha}$ $\beta$는 (1)번식을 이용하여,
$$\hat{\beta} =\frac{\sum y_{i} - \alpha \sum x_{i}}{n} , \; \hat{\beta} = \bar{y} - \hat{\alpha} \bar{x}$$
$\hat{\beta}$를 구할 수 있다.
다중선형회귀(Multiple Linear Regression)
다중 선형 회귀는 앞서이야기 한 듯이 결과변수 y에 영향을 주는 원인변수 x가 하나가 아닌 여러개인 것이다.
예를들어 연봉(y)라는 결과는 경력(x1), 학력(x2), 실적(x3), 근무시간(x4)등으로 결정될 것이다.
다중 회귀분석은 행렬(Matrix)에 대한 곱으로 식을 나타낼 수 있고, 이를 미분하여 SSE를 최소화하는 계수들의 행렬을 구할 수 있다.

여기서 우리가 사용하는 원인 변수의 개수가 k개고, 데이터의 개수가 n개라면 X 는 (n,k)형태의 행렬이 될 것이고, 각 변수에 대한 계수 $\beta$는 (k,1) 의 형태가 될 것이다. y에대한 예측값에는 오차가 존재하므로 오차 $\epsilon$값을 더해줘야 한다. 따라서 X(n,k)형태의 행렬과 $\beta$(k,1)형태의 행렬의 곱의 결과로 (n,1)형태의 행렬이 나오고, 여기에다가 오차 값을 더해주면 Y값이 된다. 수식의 표현은 다음과 같다.
※행렬이기 때문에 대문자를 사용, 모수 $\beta$가 뒤에 붙어야 행렬 곱 가능
$$ Y = X \cdot \beta + \epsilon$$
이때, 다중회귀의 SSE 함수와, SSE를 최소화 하는 $\beta$행렬은 다음과 같이 구할 수 있다.
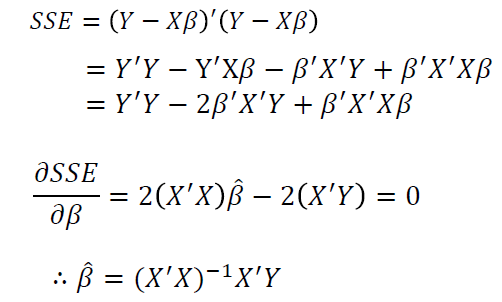
'Study > 수학과통계' 카테고리의 다른 글
| 자기회귀누적이동평균 ARIMA Model (0) | 2020.11.01 |
|---|---|
| 시계열 데이터 Time Series Data (0) | 2020.11.01 |
| Two sample t - test (0) | 2020.10.21 |
| p-value와 t분포 (0) | 2020.10.19 |
| 통계적추론 ~ 귀무가설 (0) | 2020.10.16 |


