시계열 데이터 Time Series Data

시계열 데이터 Time Series Data

시계열 데이터는 시간에 따라 연결된 데이터이다. 우리 주변에서는 이런 시계열 데이터를 많이 확인 할 수 있다.

기업의 월별 매출 관리표와 같이 시간(기간)별로 정리해 놓은 데이터가 해당되고, 음성데이터 역시 시간의 흐름 안에서 입력되는 음성이라는 생각에서 시계열 데이터에 해당된다.

이때, 데이터는 모두 같은 시간의 간격으로[등간격] 저장되어야 한다. 

정상성 Stationarity

정상성이란, 시간에 따른 데이터의 평균과 분산들값에 규칙성 없이 일정한것으로, 이전 시점의 데이터를 이용해서 다음 시점을 예측 할 수 없는상태를 뜻한다. 

시계열데이터에는 규칙성과 불규칙성이 존재한다. 하지만 완벽히 100% 불규칙적인 데이터들은 분석에 의미가 없다.

규칙성이란 보통 추세(Trend)와 계절성(Seasonality)이 해당되며, 데이터에 이렇게 평균과 분산에 변화가 있는 상태를 비정상성(Non-Stationarity)이라고 한다. 분석을 할때, 이러한 규칙성이 있는데이터들을 차분과 같은 방법을 사용해서 규칙성을 분해하고(Decomposition) 불규칙적인 데이터에대한 분석을 시행한다.

또한 평균과 분산에 변화가 완벽하게 있을 수 없기 때문에 약한 수준에서 변화가 있는 상태를 약한 정상성(Weakly Stationarity)이라고 한다. 

이미지 출처: https://stats.stackexchange.com/questions/182764/stationarity-tests-in-r-checking-mean-variance-and-covariance

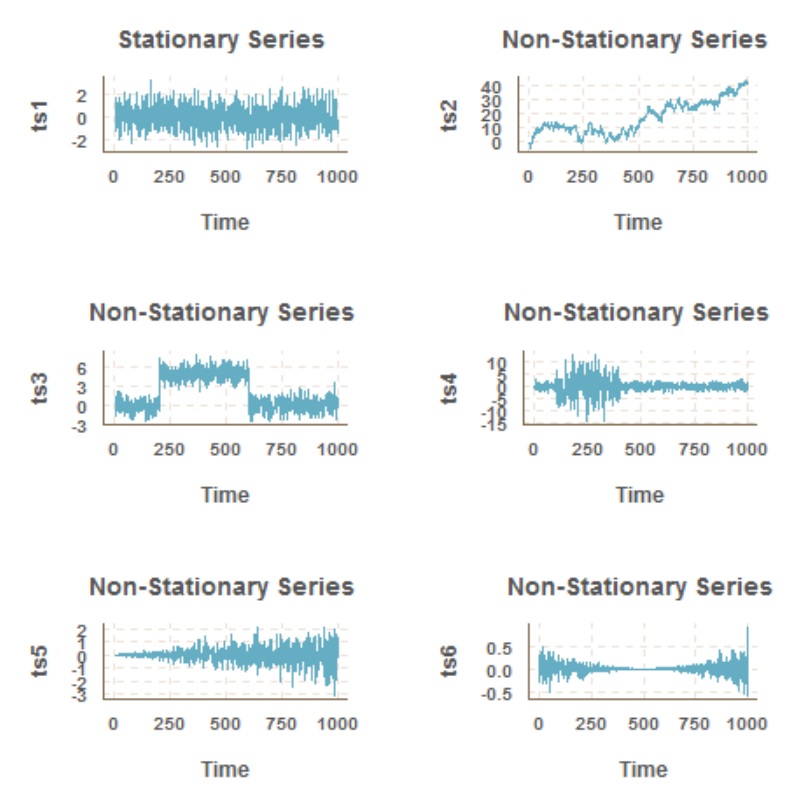
 위 이미지에서 ts1번 그래프는 일정한 평균과 분산을 가지고 있으며 증가와 감소의 주기성을 보이지만, 해당 주기가 규칙적이지 않기 때문에 정상성 데이터라고 할 수 있다.

2번 그래프는 전체적인 평균이 증가하는 추세를 보이고 있다.

3번 그래프에서는 중간에 평균이 증가한 구간을 확인할 수 있다.

4번 그래프에서는 time(250)부근에서 분산이 증가한 것을 알 수 있다.

5번은 분산이 증가하는 추세를, 6번은 분산이 감소했다가 증가하고 있다. 따라서 2~6번 그래프는 정상성 그래프라고 할 수 없다.

차분 Differencing

차분이란, 위에서 잠깐 언급한듯이 비정상성을 지닌 데이터를 정상성을 가진 데이터로 변환해주는 변수 변환 방법으로 두 시점의 차이이며 아래와 같이 표현된다.

$$\bigtriangledown Y_{t} = Y_{t} - Y_{t-1}$$

$$\bigtriangledown^{k} Y_{t} = Y_{t} - Y_{t-k}$$

또한, 아래와같이 2차 차분도 가능하다.

$$\bigtriangledown^{12} \bigtriangledown Y_{t} = \bigtriangledown^{12} ( Y_{t} - Y_{t-1} )$$

$$= \bigtriangledown^{12} Y_{t} - \bigtriangledown^{12} Y_{t-1}$$

$$= (Y_{t} - Y_{t-12}) - (Y_{t-1} - Y_{t-13})$$

$$= Y_{t} - Y_{t-1} - Y_{t-12} + Y_{t-13}$$

기존데이터(좌), $\bigtriangledown Y_{t}$차분(중), $\bigtriangledown^{12} \bigtriangledown Y_{t}$ 차분(우)

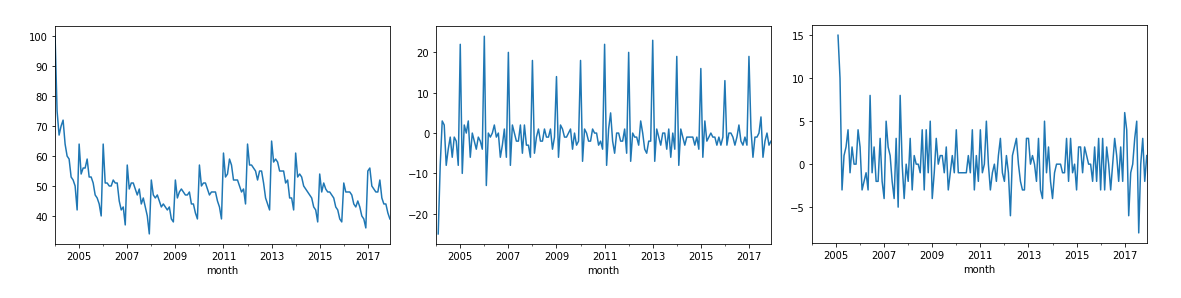
위의 그래프를 보면 가장 우측은 원데이터로, 완벽한 비정상성을 보인다.

두번째 가운데 그래프를 보면 $\bigtriangledown Y_{t}$로 한번의 차분을 시행하였으며, 여전히 고정된 간격의 주기를 보이는 계절성을 확인할 수 있다.

마지막 세번째 그래프를 보면 $\bigtriangledown^{12} \bigtriangledown Y_{t}$로 두번의 차분을 수행하였고, 비교적 정상성을 보이는 그래프를 얻어낸 것으로 확인할 수 있다.

상관관계 Correlation 과 자기상관계수 ACF(Auto Correlation Function)

상관관계는 우리가 중학교(?)때 배운것과 같이 그래프에서 x의 값과 y의 값이 특정한 상관 관계를 갖는것을 뜻한다.

양의 상관관계(좌), 음의 상관관계(우)

자기상관계수 ACF(Autocorrelation with Time lag k)는 ACF(k) 로 표현되며, t 시점과 t-k 시점에서의 관계를 뜻한다. $Cor(Y_{t}, Y_{t-k})$

t-k 시점의 데이터값과 t시점에서의 데이터값의 관계 정도를 뜻하며, 0이라면 두 데이터의 관계는 없다고 할 수 있다. 

다시말해, ACF(1)의 값이 0이 아닌 높은 숫자로 표현된다면, 바로 직전 시점(t-1)의 데이터 값으로 해당 시점(t)값을 예측 할 수 있다는 것을 뜻한다.

이때, 주의해야할 점은 만약 ACF(1)의 값이 0이 였다고 해도, ACF(2)의 값이 0이라는 보장은 없다.

t시점과 t-1시점, t-1시점과 t-2시점이 ACF 0으로 상관이 없다고 가정해도, t 시점과 t-2시점은 ACF가 0이 아닌 값으로 상관 있음을 나타낼 수있다.

마치 탈모는 한대 걸러서 나타나는것과 같이...