K - NN Algorithm
쓰옆쓰라는 말이 있다. 쓰레기 옆에는 쓰레기라는 말로 '유유상종' - 비슷한 사람끼리 친해지고 사귄다는 말이다.
K-NN 알고리즘도 이와 같다. 입력받은 데이터를 가장 성질이 가장 가까운 이웃을 비교하여 분류하는 것이다.

예를들어 평면에 위와 같이 데이터들이 분포해 있다고 가정하자,
빨간 점들은 대부분 X축 값이 크고 Y축 값이 작은 위치에 분포되어 있다.
파란 점들은 대부분 X축 값이 크고 Y축 값이 큰 위치에 분포되어 있다.
초록 점들은 X축 값이 작은 곳에 분포되어 있다.
이때, 새로운 데이터가 주어졌고, 해당 데이터는 X축 성분 값이 작고 Y축 값은 약간 높은 편이다.
최근접 이웃 알고리즘을 이용했을때, 해당 값 근처에 가장 많은 색에 따라 새로운 데이터가 분류된다. 즉, 초록색이 될 가능성이 높다.
[이웃과의 거리란?]
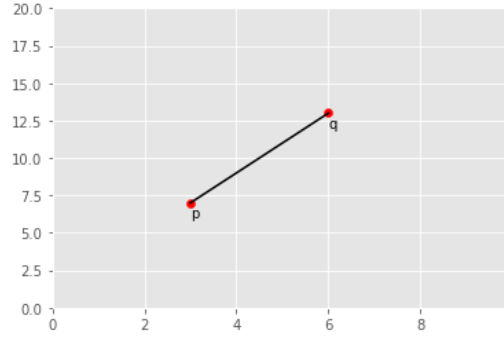
좌표 평면위의 두개의 점 : p($x_{1} , y_{1}$) q($x_{2} , y_{2}$)
두 점 사이의 거리 (d): d(p,q) = $\sqrt{( x_{2} - x_{1} )^{2} + ( y_{2} - y_{1} )^{2}}$
만약, 평면이 아닌 n차원에서의 거리를 구하고 싶다면?
p ( $x_{1} , x_{2} , \cdots , x_{n}$ )
q ( $y_{1} , y_{2} , \cdots , y_{n}$ )
d(p, q) = $\sqrt{( x_{1} - y_{1} )^{2} + ( x_{2} - y_{2} )^{2} + \cdots + ( x_{n} - y_{n} )^{2}}$
이때, k개는 확인하는 이웃의 수이다. k=1이라면 가장 가까운 이웃 하나에 따라 입력된 데이터를 분류하는 것이다.
일반적으로 3 <= k <= 10 으로 결정한다, 혹은 $\sqrt{len(train)}$ 훈련 데이터 개수의 제곱근 값을 사용한다.
만약 k가 너무 작다면 가장 근처의 데이터에 영향을 많이 받는 것이며 만약 근처 데이터가 잘못된 분류에 속해있다면 새로운 데이터도 잘못 분류될 가능성이 있다.
반대로 k가 너무 크다면 멀리 있는 데이터에도 영향을 받기 때문에 올바른 분류에 지장을 줄 수 있다.
따라서 적절한 k를 선택하는 것이 중요하다.
Data Preprocess
K-NN은 거리 유사도를 측정하기 때문에 입력변수는 연산이 가능한 양적 변수여야 하며, Scale이 동일해야 한다.
즉, Scale을 같게 해주는 표준화(혹은 정규화)과정이 필요하다.
*표준화와 정규화
1. 정규화 Normalization : 모든 값의 범위를 0 <= X <= 1 사이로 만들어 줌
$$0 \leqq \frac{X_{i} - X_{min}}{X_{max} - X_{min}} \leqq 1$$
2. 표준화 Standardization : 특정 값들이 정규분포를 따른다고 가정하고, 평균이 0 분산이 1을 갖도록 만들어 줌
$$-3 \leqq \frac{x_{i} - \bar{x}}{s} \leqq 3$$
*이때 99%의 데이터가 -3 과 3 사이에 존재
Confusion Matrix
K-NN모델을 학습하고 예측을 수행하고 오차행렬을 통해 정확도와 오차율을 판단 할 수 있다.
만약 데이터가 Y($y_{1} , y_{2} , y_{3}$)으로 분류될 수 있고 테스트 데이터에 대한 예측이 끝났다면 다음과 같은 테이블이 만들어 질 수 있다.
| Pred( $Y_{1}$ ) | Pred( $Y_{2}$ ) | Pred( $Y_{3}$ ) | |
| Real( $Y_{1}$ ) | $n_{1}$ | $n_{2}$ | $n_{3}$ |
| Real( $Y_{2}$ ) | $n_{4}$ | $n_{5}$ | $n_{6}$ |
| Real( $Y_{3}$ ) | $n_{7}$ | $n_{8}$ | $n_{9}$ |
$n_{1}$과 $n_{5}$, $n_{9}$는 실제와 예측이 맞은 데이터 개수 이다.
$n_{2}$는 실제로 $Y_{1}$인데 $Y_{2}$로 예측한 개수이고 $n_{3}$는 실제 $Y_{1}$, 예측 $Y_{3}$인 데이터 개수이다.
이런식으로 표를 다 채우면 n의 합은 데이터 개수이다.
정확도 $Accuracy = \frac{True}{N} = \frac{n_{1} + n_{5} + n_{9}}{\sum_{1}^{9} n}$
오차율 loss = 1 - Accuracy
예제 - 위스콘신 유방암 데이터
import pandas as pd
data = pd.read_csv('wisc_bc_data.csv')
data = data.drop(columns =['id'])
data.head()

먼저 데이터를 불러오고 판단에 필요없는 id 칼럼은 삭제한다.
id를 제외하고 31개의 칼럼이 있다. 여기서 diagnosis - 진단은 각각의 악성M-Malignant 양성B -Benign 으로 나뉘며 각각의 파라미터로 진단을 내리는 모델을 만들 것이다.
X = data.iloc[:,1:]
Y = data['diagnosis']
print(X.shape)
X.head()
X, 파라미터가 되는 값과 Y, 증상진단(정답) 값을 나누어 준다. 데이터의 총 개수는 569이다.
data.describe()
각 데이터의 평균, 편차 최소값 등을 확인한다. 각 변수값의 scale이 다르고 표준화나 정규화가 필요하다는 것을 알 수 있다.
X = (X - X.min()) / (X.max() - X.min())
X.describe()
정규화 식을 이용해 모든 변수값들을 0과 1사이의 값으로 변환해 준다.
sklearn의 preprocessing 을 사용해서 보다 간단하게도 할 수 있다.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,Y, test_size= 100)
#test 100개, train 469로 나누어줌
print(len(X_train),len(X_test),len(y_train),len(y_test))sklearn의 train_test_split으로 훈련용 데이터와 테스트 데이터를 나누어 준다.
test_size에 1보다 큰 정수값을 입력하면 해당 값만큼의 test 세트를 만들고,
0과 1사이의 값을 입력하면 전체 데이터에서 값만큼의 비율로 test세트를 만들어준다.
import math
print(math.sqrt(len(X_train))) #이상적인 k값?
# 3~ 29 all possible 수행앞서 말한듯이 k의 값은 3과 10 사이값이거나, 데이터 개수의 제곱근 개수이다.
여기서는 21이 나왔고 3부터 29 사이의 all possible한 경우를 실행 할 수 있다.
from sklearn import neighbors
from sklearn import metrics
knn_3 = neighbors.KNeighborsClassifier(n_neighbors=3)
knn_3.fit(X_train,y_train)
pred_3 = knn_3.predict(X_test)
pred_3_acc_matrix = metrics.confusion_matrix(y_test, pred_3)
acc = (pred_3_acc_matrix[0,0] + pred_3_acc_matrix[1,1])/pred_3_acc_matrix.sum()
print(acc)
print(pred_3_acc_matrix)
k = 3일때, 정확도는 0.95이다. [실제B, 예측B : 57] [실제B, 예측M : 1] [실제M, 예측 B : 4] [실제 M, 예측 M : 38]
k = 5일때 같은 정확도 0.95를 보였고, k = 7일때 0.97을 보였다. 하지만 k = 9 일때 0.94로 오히려 떨어졌다.
knn_21 = neighbors.KNeighborsClassifier(n_neighbors=21)
knn_21.fit(X_train,y_train)
pred_21 = knn_21.predict(X_test)
pred_21_acc_matrix = metrics.confusion_matrix(y_test, pred_21)
acc = (pred_21_acc_matrix[0,0] + pred_21_acc_matrix[1,1])/pred_21_acc_matrix.sum()
print(acc)
print(pred_21_acc_matrix)
훈련 데이터 개수의 제곱근 값인 21을 입력했을때 결과이다. 0.93으로 k=3 , k=5 보다 낮은 정확도를 보였다.
이후 23, 25 ... k값을 늘려갈 수록 정확도는 떨어졌다. 이로써 k = 7이 가장 이상적이다라는 결론을 내렸다.
'Study > 수학과통계' 카테고리의 다른 글
| 베르누이 분포, 이항분포, Random Walk (1) | 2020.11.10 |
|---|---|
| 적분 in Python, 몬테카를로 방법 Monte-Carlo Method (0) | 2020.11.10 |
| 자기회귀누적이동평균 ARIMA Model (0) | 2020.11.01 |
| 시계열 데이터 Time Series Data (0) | 2020.11.01 |
| 선형회귀분석 Linear Regression , SSE, OLS (0) | 2020.10.23 |


