표준 정규 분포의 적분
표준 정규 분포 확률 밀도 함수
$$ f(x) = \frac{1}{\sqrt{2 \pi}} e^{- \frac{1}{2} x^{2} } $$

1.96~ 6까지의 적분 일반적인 적분식으로 계산하자면,
$$\int_{1.96}^{6} \frac{1}{\sqrt{2 \pi}} e\left( - \frac{x^{2}}{2} \right) \, dx$$

위 평면의 1.96부터 6까지의 초록색 막대그래프들의 넓이의 합을 구하면 된다.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
#Trapezoidal Rule
def normal_pdf(x,m = 0, std = 1):
return np.exp(- ( (x - m) **2 ) / (2 * ( std ** 2 ) ) ) / ( np.sqrt( 2 * np.pi) * std )
x = np.linspace(1.96, 6, 10000)
summ = 0
height = (6 - 1.96) / 10000
for i in range(0, len(x)):
t = normal_pdf(x[i]) * height
summ += t
print('integral value :', summ)
k = np.random.normal(0,1,size = 10000)
graph_range_x = np.linspace(-6,6,10000)
graph_range_y = normal_pdf(graph_range_x)
plt.figure()
plt.plot(graph_range_x,graph_range_y)
plt.hist(k,bins =50, density=True, histtype='stepfilled',color='C2')
plt.axvline(1.96,color = 'r')
plt.axvline(6,color = 'r')
plt.show()1. 구하고자 하는 범위(1.96~6)까지를 빽빽하게 나눈다. # x = np.linspace(1.96, 6, 10000)
2. 넓이를 더해갈 변수를 생성하고, 고정된 가로축을 설정해준다. # summ = 0 , hegiht = (6 - 1.96) / 10000
3. x array의 확률밀도함수값과 높이를 곱해서 각각의 막대그래프 넓이를 구해주고 summ에다가 더해준다.
결과값:
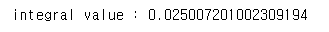
[k = np.random.normal 부터는 위에 그래프 출력 문장]
몬테카를로 방법 MonteCarlo Method
몬테카를로 방법은 난수를 이용해서 함수의 값을 확률적으로 계산하는 알고리즘을 부르는 용어이다. -위키백과-
난수를 통해 평면에서의 넓이를 구할 수 있다.

위 그림에서 두개의 수직선은 1.96~ 6까지의 범위를 나타낸다. 평행선은 1.96일때 표준정규분포 확률밀도함수값이다.
각각의 선을 이었을때 만들어지는 사각형을 확인할 수 있다.
난수를 하나 만든다. 만약 난수가 이 사각형 범위 안에 있다면 hit, 밖이라면 miss다.
난수를 계속해서 발생시키고, 전체 난수개수 n개 중 hit 비율을 구한다.
사각형 넓이에서 위에서 계산한 난수비율을 곱하면 1.96~6까지의 확률밀도함수 적분값(확률값)을 구할 수 있다.
사각형 넓이 S , 난수 개수 n, 히트비율 hit_rate = $\frac{hit}{n}$, 적분값 = S x hit_rate
# Monte-Carlo method
n1 = 100
n2 = 1000
n = 10000
x_range = np.linspace(1.96,6,n )
y_range = np.linspace(0,normal_pdf(1.96), n)
square = (6 - 1.96) * normal_pdf(1.96)
hit = 0
for i in range(n):
x = np.random.choice(x_range, 1)
y = np.random.choice(y_range, 1)
if y <= normal_pdf(x):
hit += 1
if i == 99:
print('n :{} , hit_rate : {} integral_value : {}'.format(i, hit/i, square * (hit / i)))
if i == 999:
print('n :{} , hit_rate : {} integral_value : {}'.format(i, hit/i, square * (hit / i)))
print('n :{} , hit_rate : {} integral_value : {}'.format(n, hit/n, square * (hit / n)))
1. 난수개수 설정한다. -> 10000개
2. 난수개수에 맞는 x축 범위 설정, y축 범위 설정 (y축 범위는 사각형의 높이에 해당한다)
3. 사각형 넓이를 설정해준다. (x축 1.96~6 : 가로(6 - 1.96) y축 높이 -> 가장 큰 y값 : normla_pdf(1.96)
4. 10000번 동안 x_array와 y_array에서 하나씩 랜덤하게 choice한다. choice된 값이 각각 평면 좌표
(x_choice, y_choice)
5. 만약 choice된 y값이 확률밀도함수에서의 x_choice값 보다 작으면(그래프 안에 있다면) hit rate에 1을 추가한다.
반복반복
결과:

위 정적분 값: 0.025007201002309194
n의 크기가 커질 수록 정확한 값과 가까워지는 것을 확인 할 수 있다.
실전예제 - 별넓이 구하기

별 좋아하시나요? 전 좋아합니다 그림판에서 만든 별이에요
몬테카를로 방법을 이용해서 일반 1차 그래프가 아닌 둥근모양, 별 모양 등 평면에서의 여러 모양의 넓이를 추정할 수 있다. 현실에서 암세포의 크기를 추정할때 위와같은 방법을 사용할 수 있다고 한다.
위의 몬테카를로 알고리즘과 같은 방법을 사용하지만, hit 판정에 대한 새로운 알고리즘이 필요하다.
1. 이미지 불러들이기, 정보확인
import matplotlib.pyplot as plt
img = plt.imread('star.png')
print(img.shape)
plt.imshow(img, cmap = 'gray')

hit와 miss의 차이점에 대한 판단 알고리즘은 각자 생각나는 것이 있을 것이다.
고안할 수 있는 알고리즘:
1. 해당좌표에서 가로축과 세로축으로 선을 긋는다.
2. 만약 hit라면, 상하좌우 방향으로 도형의 외각 선과 만나는 점이 존재한다. (위 그림 참조)
3. miss라면, 어느쪽이든 만나지 않는 점이 하나 이상 존재한다.
#method1
img = plt.imread('star.png')
img = img[:,:,0] #use 1 filter
img = -img + 1 #흑 백 전환 0 -> 1 , 1 -> 0
print(np.unique(img), img[:10,0])
n = 100000
x = np.random.randint(img.shape[1],size = n)
y = np.random.randint(img.shape[0], size = n)
def check_func(arr,x,y):
return (np.sum(arr[:y,x]) * np.sum(arr[y:,x]) * np.sum(arr[y,:x]) * np.sum(arr[y, x:])) != 0 #up, down, left, right
hit = 0
for i in range(n):
if check_func(img,x[i],y[i]) == True:
hit += 1
img[y[i],x[i]] = 1
square = img.shape[0] * img.shape[1]
hit_rate = hit / n
print(square, hit, square * hit_rate)
img = -img + 1
plt.imshow(img, cmap = 'gray')같은 알고리즘으로 두가지 구현법이 있다.
첫번째 방법 : 이 방법은 이미지에서 검정색(별의 선부분)= 1, 흰색(배경부분) = 0인 성질을 이용한다.
먼저 이미지는 0과 1로만 이루어져 있다. 검정색은 0, 흰색은 1로 되어 있다. (아래 이미지 좌측)
이것을 -1을 곱하고 1을 더해줘서 0을 1로, 1을 0으로 바꿔준다.(아래 이미지 중앙)
n개의 샘플을 설정해주고, 이미지 shape(x-scale, y-scale)범위의 난수를 각각 생성한다.
check func은 검정색 선 부분을 1로 바꿔주었기 때문에
만약 히트라면, 상하 좌우에는 반드시 선이 존재하고, 상하좌우 각각 픽셀값을 더한 값은 1보다 크게된다.
따라서 이 값들을 곱할경우 0이 아닌 값이 나오게 된다.
반대로 미스라면, 상하좌우 중 하나는 반드시 선이 존재하지 않고, 0값이 존재한다.
따라서 이값들을 곱할경우 0이 된다.
그 다음은 몬테카를로 알고리즘에 맞춰 수행하면 되고,
결과 확인을 위해 hit면 이미지 픽셀값을 1로 설정한다.
그리고 반복문을 완료하면, 다시 흰색과 검정색을 1과 0으로 바꿔줘서 결과를 확인할 수 있다.(아래 이미지 우측)

출력값:
평면 넓이: 112560 hit개수: 28605 별모양 면적: 32197.788000000004
#method 2
img = plt.imread('star.png')
img = img[:,:,0]
shape = img.shape
n = 100000
x = np.random.randint(shape[1],size =n)
y = np.random.randint(shape[0],size =n)
hit = 0
for i in range(n):
x_idx = np.where(img[y[i],:] == 0)
y_idx = np.where(img[:,x[i]] == 0)
try:
x_cond = ( len(x_idx) > 0 ) and (np.max(x_idx) >= x[i]) and (np.min(x_idx) <= x[i])
y_cond = ( len(y_idx) > 0 ) and (np.max(y_idx) >= y[i]) and (np.min(y_idx) <= y[i])
except:
x_cond , y_cond = 0, 0
if x_cond and y_cond:
hit += 1
img[y[i],x[i]] = 0
square = shape[0] * shape[1]
hit_rate = hit / n
area = square * hit_rate
print('평면 넓이: {}, hit개수: {}, 별모양 면적: {}'.format(square, hit, area))
plt.imshow(img,cmap ='gray')
두번째 방법: np.where()을 이용해 index값 비교를 사용한다.
1. x[i]와 y[i] 는 각각 평면에서의 위치이다. (x[i],y[i])
2. x_idx 는 y[i]값에서의 수평선 중에, 0(검정색)인 값이다. y_idx는 x가 x[i]인 수직선에서 0인 값들의 위치이다.
3. x_cond은 수평선에서 검정 선과 한번이라도 마주친다면, len(x_cond)은 0보다 클것이다.
x[i] 우측에 선과 접점이 있다면, max(x_idx)는 x[i]보다 클 것이다.
x[i] 좌측에 선과 접점이 있다면, min(x_idx)는 x[i]보다 작을것이다.
4. y_cond도 마찬가지이며, 접점이 없는경우 오류가 발생하기에 try문을 사용했다.
반대로 오류가 발생하는경우 접점이 없는 경우기 때문에 cond값에 False 를 의미하는 0을 입력했다.
그 후는 위와 같은 알고리즘이다.
출력값:
평면 넓이: 112560, hit개수: 29020, 별모양 면적: 32664.912

'Study > 수학과통계' 카테고리의 다른 글
| 베르누이 분포, 이항분포, Random Walk (1) | 2020.11.10 |
|---|---|
| ML : K- 최근접 이웃 K-NN(K-Nearest Neighbor Algorithm) (0) | 2020.11.07 |
| 자기회귀누적이동평균 ARIMA Model (0) | 2020.11.01 |
| 시계열 데이터 Time Series Data (0) | 2020.11.01 |
| 선형회귀분석 Linear Regression , SSE, OLS (0) | 2020.10.23 |


