오늘은 파이썬의 statsmodels에 있는 OLS Model에 대해 포스트 한다.
예제는 맨 마지막에 넣었다.
OLS모델을 통해 살펴볼 것들
1. OLS Model은 선형 회귀분석에 있어서 각각의 독립변수 $x_{i}$가 종속변수 y에 영향이 있는지 단적으로 확인 할 수 있다. (귀무가설과 대립가설 - t분포와 p value)
2. 다른 독립변수들을 배제하고 특정 변수에 있어서 독립변수에 영향을 주는지 확인할 수 있다.(Regress out)
3. 회귀 방정식에서 각 변수의 계수값을 알 수 있다.
4. 해당 방정식으로 데이터들을 얼마나 설명할 수 있는지
5. 명목변수의 encoding
데이터
statsmodel에 보면 다음과 같은 문구가 있다.
"statsmodels supports specifying models using R-style formulas and pandas DataFrames. "
즉, r형식의 함수와 pandas 형태의 데이터를 지원한다는 것인데, 홈페이지에서 statsmodel.dataset.get_rdataset 함수를 사용한 것을 봤을때 rdataset을 가져오는것을 지원하나보다.
혹은 numpy로 대체할 수 있다. numpy를 사용할 경우, 따로 원인변수를 add_constant를 통해 객체를 만들어야 한다.
자세한 사항은 statsmodel 홈페이지 참조: www.statsmodels.org/stable/index.html
Introduction — statsmodels
statsmodels is a Python module that provides classes and functions for the estimation of many different statistical models, as well as for conducting statistical tests, and statistical data exploration. An extensive list of result statistics are available
www.statsmodels.org
하지만 오늘 사용한것은 pandas datasets이다. pandas datasets을 이용할 경우, 데이터를 따로 statsmodel 객체로 만들 필요가 없기 때문에 보다 간단하다.
식표현
우선, 다중 회귀 방정식에 대해서 다음과 같이 설정할 수 있다.
$$y_{i} = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} \cdots \beta_{n} x_{n} + \epsilon_{i}$$
Python의 statsmodels.formula.api에 있는 ols를 이용하면 다음과 같이 표현 할 수 있다.
from statsmodels.formula.api import ols
model = ols(formula = 'Y ~ X1 + X2 + ... + Xn',data = data).fit()
print(model.summary())
파라미터 formula는 '예측하고자 하는 칼럼 이름 ~ 원인이되는 칼럼 이름(+로 연결)'을 설정해주고,
data 에는 내가 가지고 있는 Pandas DataFrame을 넣어주면 된다.
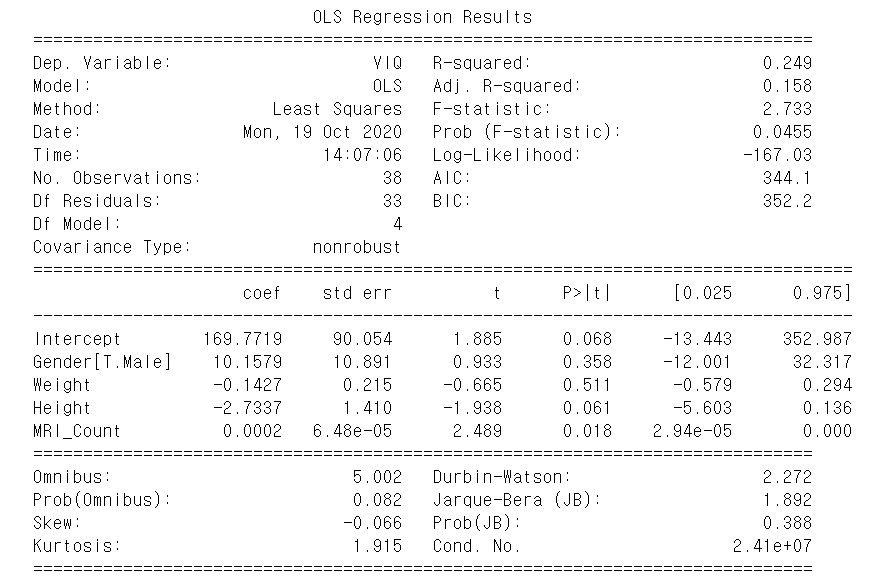
예제에서 사용한 데이터와 summary 결과이다.
Dep.Variable 은 내가 예측하고자한 Y값 데이터이다.
Residuals 는 n - k 값으로 여기서 n은 데이터 개수, k는 미지수의 개수이다.
R-squared 는 전체 변동 중에 n%를 설명할 수 있다는 뜻으로, SSR / SST 값이며 여기서 SST 는 SSR + SSE로 표현된다.
이때, 값은 0< $R^{2} = \frac{SSR}{SST}$ < 1
※SST : Sum of Squared Total - 총 변동 , SSR : Sum of Squared Residuals - 설명 안된 변동, SSE: Sum of Squared Error - 설명 된 변동 // 변동이라는 말이 이해가 안돼서 오차로서 변동을 이해했다.
coef - 각 변수에 대한 계수값
t , P>|t| - t값과 p-value
예제
오늘 사용한 표본 데이터는 사람들의 성별, 키, 몸무게, 뇌크기, VIQ, PIQ, FSIQ이며 키와 몸무게, 뇌크기의 차이를 고려하지 않고 성별의 차이로만 VIQ차이를 확인 할 것이다.
import pandas as pd
import numpy as np
from statsmodels.formula.api import ols
data_df = pd.read_csv('brain_size.csv',sep = ';')
data_df.head()
먼저 각 모듈을 import 해주고, csv파일을 DataFrame 객체로 선언해준다.
group_M_VIQ = data_df[data_df['Gender'] == 'Male']['VIQ']
group_F_VIQ = data_df[data_df['Gender'] == 'Female']['VIQ']
print(group_M_VIQ.mean(), group_F_VIQ.mean())
#115.25 109.45
# 남자의 평균 VIQ가 높다
먼저 t-test로 성별에 따른 VIQ차이를 확인해 보자.
성별에 따른 VIQ차이를 확인할 것이므로 각 성별에 따라 VIQ 평균을 구해준다.
결과 값이 남 - 115.25 , 여 - 109.45 로 나왔다. 이로부터 '남자의 평균 VIQ가 여자보다 높다'라는 대립가설을 세울 수 있고, '남자와 여자의 VIQ는 차이가 없다'라는 귀무가설을 세울 수 있다.
from scipy import stats
value_t , value_p = stats.ttest_ind(group_M_VIQ,group_F_VIQ) #H0 : 남자와 여자의 평균 VIQ는 차이가 없다
reliability = 1 - value_p
print(value_t,value_p,reliability)
#0.7726161723275011 0.44452876778583217 0.5554712322141678
#p-value 0.4, H0 기각하기 어려움
계산된 p-value는 0.44로 자신이 신뢰구간을 얼마로 설정하느냐에 다르겠지만, 일반적으로 0.44로귀무가설을 기각하기에는 많은 위험이 따른다. 즉, '성별에 따른 VIQ차이는 없다'로 결론내릴 수 있다.
이제, OLS 분석으로 넘어가자
data_df.info()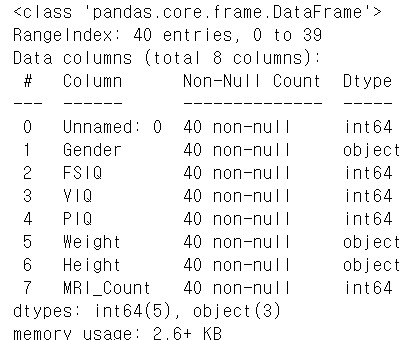
먼저 기본적인 데이터의 정보를 확인했다. int 혹은 float으로 표현되어야할 Weight와 Height 칼럼이 object 형태로 되어있고, 확인해보니 결손 데이터가 '.'로 표기되어 있었다.
print(data_df[data_df[['Height','Weight']] == '.'].count())
dot_idx = data_df[(data_df['Height'] == '.') | (data_df['Weight'] == '.')].index
data_df = data_df.drop(dot_idx)
print(data_df[data_df[['Height','Weight']] == '.'].count())
data_df = data_df.astype({'Height':float,'Weight':float})
data_df.info()
Height와 Weight에서 '.'의 index값을 받고, 이를 이용해서 삭제해 주었다. 이후 각각의 데이터 타입을 astype으로 float으로 바꿔주었다.
model = ols(formula = 'VIQ ~ Gender + Weight + Height + MRI_Count',data = data_df).fit()
print(model.summary())
이후 ols model을 만들고, Weight, Height, MRI_Count를 원인 변수로 같이 넣어서 regress out 해주고, summary 표를 확인했다.

결과의 p-value를 확인했을때, 마찬가지로 일반적인 유의수준을 훨씬 넘어서는 값이 나왔고 마찬가지로 각 성별의 비교는 무의미하다고 할 수 있다.
이때, Gender[T.Male]으로 표기된 것을 보아 Male = 1, Female = 0으로 Encoding 된 것을 알 수 있다.
즉 회귀 방정식은 다음과 같다.
$$VIQ = 169.7719 + 10.1579 \cdot Male - 0.1427 \cdot Weight - 2.7337 \cdot Height + 0.0002 \cdot MRICount$$
하지만 이것은 단순 OLS 실습을 위해 사용한것으로 각각의 p-value와 R square 값을 확인했을때, 해당 식은 크게 의미가 없다는 것을 알 수 있다.
마지막으로 예측에 사용된 feature, 예측된 VIQ 값, 실제 VIQ값, 오차들을 이용해 새로운 DataFrame을 만들어 보자.
data = pd.DataFrame(data_df[['Gender','Weight','Height','MRI_Count','VIQ']])
def pred_VIQ_byGender(row):
if row.Gender == 'Male':
return 169.7719 + 10.1579 - (0.1427 * row.Weight) - (2.7337 * row.Height) + (0.0002 * row.MRI_Count)
else:
return 169.7719 - (0.1427 * row.Weight) - (2.7337 * row.Height) + (0.0002 * row.MRI_Count)
data['Pred_VIQ'] = data.apply(pred_VIQ_byGender,axis = 1)
data['Error'] = data.VIQ - data.Pred_VIQ
data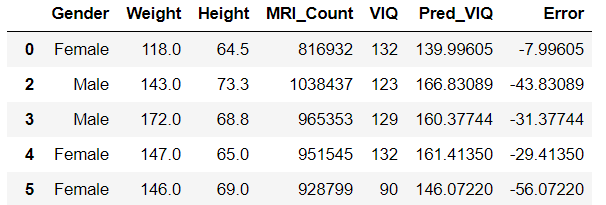
'Study > Python' 카테고리의 다른 글
| Random 개요, 컴퓨터의 난수 생성 (0) | 2020.11.10 |
|---|---|
| 파이썬 가상환경 tf1.x버전 다운로드 파이참 연결 (0) | 2020.10.20 |
| 1. 계산기 만들기 (1) | 2020.10.13 |

